Prolog est un langage déclaratif qui décrit les problèmes plutôt que d’indiquer à la machine comment trouver la solution. La description se fait à travers l’écriture de prédicats logics et a pour avantage de faire réfléchir le programmeur sur la modélisation du problème…. C’est mon langage préféré mais je n’ai pas l’occasion de m’en servir dans ma vie professionnelle. La faute à ce langage à la mode qu’était Java et avec lequel j’ai débuté ma carrière il y a plus de 10 ans. Dans ce blog donc point de référence à Prolog jusqu’à aujourd’hui et ce billet sera pour corriger ce défaut.

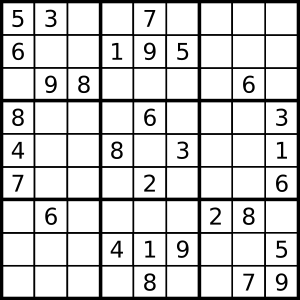
Pour disserter sur Prolog j’ai choisi un exercice facile pour montrer le mécanisme de recherche de Prolog (la base du calcul  des prédicats)  et la programmation par contrainte qui permet de réduire grandement le temps de calcul. Cet exercice est le Sudoku 9×9.

Aperçu de Prolog

Prolog (Programmation Logique) peut être vu comme une base de connaissances où l’on ajoute des prédicats et des règles de déductions entre ces prédicats. Par exemple on peut dire à Prolog que Pierre est un garçon. Pour cela il suffit de décider que garçon(X) est un prédicat qui dit que X est un garçon où X est une variable. On apprend à Prolog que le prédicat garçon(X)  est vrai si X prend la valeur Pierre. En d’autre terme on apprend à Prolog que si X vaut Pierre alors X est un garçon. Ce qui s’écrit

garçon(X) :- X = 'Pierre'

C’est ce qu’on appelle une règle. On peut ajouter autant de règles que l’on veut. On ainsi dire que Paul est un garçon aussi.

garçon(X) :- X = 'Paul'

On peut alors interroger Prolog en lui demandant qui sont les garçons ? i.e on demande à Prolog de rendre vrai le prédicat  garçon(Y) où Y est une variable, alors Prolog répondra que pour cela il faut que Y prenne la valeur de ‘Pierre’ ou ‘Paul’.

Et la programmation dans tous ça ? Si on ajoute un prédicat qui dit que Pierre et Annie sont nos amis. Cela se fait par les instructions suivantes:

ami('Pierre').
ami('Annie')

On peut demander à Prolog les amis qui sont des garçons.
ami(X),garçon(X)

Prolog répond que X doit prendre la valeur de Pierre. On a l’intuition que cette manière de programmer en est bien une, on arrive à résoudre des problèmes via uniquement leur description qui devient alors le seul objectif du programmeur. La résolution c’est le travail de Prolog. Pour terminer de se convaincre on va illustrer par la résolution du sudoku 9×9.

Sudoku 9×9

Nous allons définir les valeurs possibles sur notre grille de sudoku. Il s’agit des nombre de 1 à 9. Les règles suivantes permettent de le faire en utilisant le langage de base et les listes.

takeout(A,[A|B],B).
takeout(A,[B|C],[B|D]):- takeout(A,C,D).
valeur(X):-takeout(X,[1,2,3,4,5,6,7,8,9],_).


Ainsi si on interroge Prolog en lui demandant de rendre vrai le prédicat valeur(X) alors on obtient les réponses

X=1;
X=2;
...
X=9


Ces valeurs doivent être placées dans les carrés 3×3. Nous définissons ainsi un tel carré par

carre([[A,B,C],[D,E,F],[G,H,I]]):-
valeur(A),valeur(B),valeur(C),
valeur(D),valeur(E),valeur(F),
valeur(G),valeur(H),valeur(I)

où la liste en argument contient les valeurs lignes par lignes.

A ce stade une interrogation du prédicat carré(X) nous renvoie toutes les valeurs sans respecter les règles du sudoku. Par exemple X prend la valeur d’une matrice remplie de 1. Pour continuer il faut décrire les règles d’unicité du sudoku.

L’unicité des nombres dans les carrés 3×3 se fait avec les prédicat suivants:

different(_,[]).
different(A,[B|C]):-
A = B,
different(A,C).


tous_differents([]).
tous_differents([A|R]):-
different(A,R),
tous_differents(R).


Un carré 3×3 doit être remplis des valeurs de 1 à 9 mais toutes les valeurs doivent être distinctes. Donc le prédicat carré(X) devient:

carre([[A,B,C],[D,E,F],[G,H,I]]):-
valeur(A),valeur(B),valeur(C),
valeur(D),valeur(E),valeur(F),
valeur(G),valeur(H),valeur(I),
tous_differents([A,B,C,D,E,F,G,H,I]).


On remarque que la première solution met quelques instants avant d’être affichée. Pourquoi ? On touche ici à l’implémentation de la programmation logique sur nos processeur qui sont des machine de turing. En logique classique il n’y a pas de notion de séquence d’execution mais dans l’implémentation de Prolog il y a un ordre d’execution. Dans notre code la valorisation des cases se fait avant l’exécution du prédicat tous_differents/1 donc le programme énumère les carré jusqu’à ce qu’il en trouve un qui vérifie le prédicat tous_différents/1 ! Cela peut être long….

Discriminer au plus tôt

En règle générale il faut aider Prolog à discriminer les solutions potentielles le plus tôt possible. Dans notre cas il faut poser les prédicats qui imposent les règles d’unicité en premier. Notre prédicat devient


carre([[A,B,C],[D,E,F],[G,H,I]]):-
tous_differents([A,B,C,D,E,F,G,H,I]),
valeur(A),valeur(B),valeur(C),
valeur(D),valeur(E),valeur(F),
valeur(G),valeur(H),valeur(I).

Ce code est juste en théorie. Il fonctionne quand on passe des valeurs a carré/1 et qu’on demande de vérifier si le prédicat est vrai. Mais on veut aussi que cela marche en recherche de solution i.e. en passant une variable en argument de carré/1. Là ça coince, le prédicat est toujours faux !

La faute en incombe au test de différence dans

different(A,[B|C]):-
A = B,
different(A,C).


Comme les variables ne sont pas valorisées, le test est faux. On aimerait bien que Prolog pose simplement la contrainte de différence et que, plus tard lors de l’exécution des prédicats de valorisation, les chemins sans solutions soient évités. Pour cela on va utiliser la programmation logique par contrainte.

Programmation logique par contrainte

Le compilateur gprolog est livré en standard avec le module de contrainte sur les domaines finis. Le compilateur multithreadé SWI-Prolog nécessite quant à lui le chargement manuel du module de contrainte sur les domaines finis en faisant:

use_module(library(clpfd)).

On utilise ensuite le prédicat infixé spécial au domaine fini pour spécifier la différence.Ainsi:

different(A,[B|C]):-
A #= B,
different(A,C).


Dès lors prédicat carre/1 est quasi instantané et donne les solutions des carré 3×3.

La solution finale de cet exercice est alors une question réglée:

takeout(A,[A|B],B).
takeout(A,[B|C],[B|D]):- takeout(A,C,D).
valeur(X):-takeout(X,[1,2,3,4,5,6,7,8,9],_).

different(_,[]).
different(A,[B|C]):-
    A #= B,
    different(A,C).

tous_differents([]).
tous_differents([A|R]):-
    different(A,R),
    tous_differents(R).

carre([[A,B,C],[D,E,F],[G,H,I]]):-
    tous_differents([A,B,C,D,E,F,G,H,I]),
    valeur(A),valeur(B),valeur(C),
    valeur(D),valeur(E),valeur(F),
    valeur(G),valeur(H),valeur(I).
concat_trois([A1,B1,C1],[A2,B2,C2],[A3,B3,C3],X):-
    X = [A1,B1,C1,A2,B2,C2,A3,B3,C3].

lignes_differentes([[A1,A2,A3],[B1,B2,B3],[C1,C2,C3]]):-
    concat_trois(A1,B1,C1,L1),
    tous_differents(L1),
    concat_trois(A2,B2,C2,L2),
    tous_differents(L2),
    concat_trois(A3,B3,C3,L3),
    tous_differents(L3).

colonnes_differentes([A,D,G]):-
    A = [[A1,A2,A3],[A4,A5,A6],[A7,A8,A9]],
    D = [[D1,D2,D3],[D4,D5,D6],[D7,D8,D9]],
    G = [[G1,G2,G3],[G4,G5,G6],[G7,G8,G9]],
    tous_differents([A1,A4,A7,D1,D4,D7,G1,G4,G7]),
    tous_differents([A2,A5,A8,D2,D5,D8,G2,G5,G8]),
    tous_differents([A3,A6,A9,D3,D6,D9,G3,G6,G9]).

sudoku([[A,B,C],[D,E,F],[G,H,I]]):-

    lignes_differentes([A,B,C]),
    lignes_differentes([D,E,F]),
    lignes_differentes([G,H,I]),

    colonnes_differentes([A,D,G]),
    colonnes_differentes([B,E,H]),
    colonnes_differentes([C,F,I]),

    carre(A),carre(B),carre(C),
    carre(D),carre(E),carre(F),
    carre(G),carre(H),carre(I).